Ok...
Kita akan mencari nilai limit trigonometri yang berbentuk pecahan...
Mari kita kerjakan...!!
Berikut adalah langkah-langkahnya...
Ubah dulu bentuk pembilangnya, hilangkan bagian pengurangan, sehingga semuanya dalam bentuk perkalian..
Pembilangnya adalah 1 - cos2x.
Bentuk inilah yang diubah.
Kita gunakan yang cos 2x = 1 - 2sin²x
Mengapa gunakan yang ini?
Karena jika kita gunakan 2cos²x - 1, hasilnya masih ada bentuk pengurangan.
Mari kita buktikan!!
Lihat bagian pembilang ya!
= 1 - cos2x
= 1 - (2cos²x - 1)
= 1 - 2cos²x + 1
= 2 - 2cos²x
Nah..
Masih ada bentuk pengurangan...
Kita hindari yang seperti ini untuk memudahkan perhitungan.
Jadi gunakan 1 - 2sin²x.
Sekarang tan x diubah menjadi sin x/cos x
Menggunakan sifat pembagian pecahan, maka cos x berada pada posisi pembilang sekarang, sedangkan sin x tetap di bawah.
sin²x dipecah = sin x. sin x
Angka 2 bisa dibawa ke depan.
Sehingga kita peroleh hasilnya adalah 2.
Kita akan mencari nilai limit trigonometri yang berbentuk pecahan...
Mari kita kerjakan...!!
Soal :
1. Hitunglah nilai limit berikut!
1. Hitunglah nilai limit berikut!
Berikut adalah langkah-langkahnya...
Ubah dulu bentuk pembilangnya, hilangkan bagian pengurangan, sehingga semuanya dalam bentuk perkalian..
Pembilangnya adalah 1 - cos2x.
Bentuk inilah yang diubah.
Cos 2x = 2cos²x - 1
Cos2x = 1 - 2sin²x
Kita gunakan yang cos 2x = 1 - 2sin²x
Mengapa gunakan yang ini?
Karena jika kita gunakan 2cos²x - 1, hasilnya masih ada bentuk pengurangan.
Mari kita buktikan!!
Lihat bagian pembilang ya!
= 1 - cos2x
= 1 - (2cos²x - 1)
= 1 - 2cos²x + 1
= 2 - 2cos²x
Nah..
Masih ada bentuk pengurangan...
Kita hindari yang seperti ini untuk memudahkan perhitungan.
Jadi gunakan 1 - 2sin²x.
- cos2x diganti dengan 1 - 2sinx
Sehingga bentuk pembilangnya tidak ada pengurangan atau penjumlahan. Hanya perkalian saja..
Usahakan selalu membuat bentuk seperti ini untuk memudahkan perhitungan.
Sekarang tan x diubah menjadi sin x/cos x
Menggunakan sifat pembagian pecahan, maka cos x berada pada posisi pembilang sekarang, sedangkan sin x tetap di bawah.
sin²x dipecah = sin x. sin x
Angka 2 bisa dibawa ke depan.
Ingat!
sinx/x = 1 jika x-nya mendekati nol
sinx/sinx = 1
Ingat!
cos 0 = 1
Sehingga kita peroleh hasilnya adalah 2.
Baca juga :
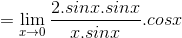
Post a Comment for "Limit (1-cos2x)/x.tanx . X-nya mendekati nol"