Sebelumnya kita sudah membahas cara mencari f(x) jika diketahui fungsi komposisi (fog)(x) dan g(x).
Sekarang kita coba kebalikannya.
Soal ini adalah kebalikan dari soal berikut :
Masih ingat dengan pengertian fungsi komposisi (fog)(x)?
Diketahui :
Sekarang kita coba kebalikannya.
Soal :
1. Jika (fog)(x) = 10x - 5 dan f(x) = 2x + 1, hitunglah fungsi g(x)!
1. Jika (fog)(x) = 10x - 5 dan f(x) = 2x + 1, hitunglah fungsi g(x)!
Soal ini adalah kebalikan dari soal berikut :
Jika (fog)(x) = 10x-5 dan g(x) = 5x-3, hitunglah nilai f(x)!
Silahkan lihat soal diatas untuk referensi pembelajaran yang lain.Masih ingat dengan pengertian fungsi komposisi (fog)(x)?
(fog)(x) artinya, setiap nilai x pada f(x) diganti dengan g(x).
Diketahui :
- (fog)(x) = 10x - 5
- f(x) = 2x + 1
Karena g(x) tidak diketahui, maka misalkan :
- g(x) = a
Masuk kembali ke fungsi komposisinya.
(fog)(x) = f [g(x)]
(fog)(x) = f [g(x)]
- Jadi, g(x) akan menggantikan setiap nilai x pada f(x) ya.
- Kemudian, diatas sudah dimisalkan kalau g(x) = a.
Sehingga :
(fog)(x) = f [a]
- (fog)(x) = 10x - 5
- f(x) = 2x + 1
10x - 5 = 2a + 1
Perhatikan :
- (fog)(x) diganti dengan 10x - 5
- f(x) = 2x + 1
Tapi karena dimintai f(a), maka ganti x pada f(x) dengan a
10x - 5 = 2a + 1
- pindahkan +1 ke ruas kiri menjadi -1
10x - 5 - 1 = 2a
10x - 6 = 2a
- Untuk mendapatkan x, bagi 10x dan -6 dengan 2
5x - 3 = a
Ingat!!
Diatas dimisalkan bahwa g(x) = a
Dan a = 5x - 3
Sehingga :
g(x) = a
g(x) = 5x - 3
Nah, inilah g(x) yang dicari.
Hasilnya sama seperti soal sebelumnya..
Silahkan baca di :
Jika (fog)(x) = 10x-5 dan g(x) = 5x-3, hitunglah nilai f(x)!
Diatas dimisalkan bahwa g(x) = a
Dan a = 5x - 3
Sehingga :
g(x) = a
g(x) = 5x - 3
Nah, inilah g(x) yang dicari.
Hasilnya sama seperti soal sebelumnya..
Silahkan baca di :
Jika (fog)(x) = 10x-5 dan g(x) = 5x-3, hitunglah nilai f(x)!

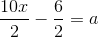
Post a Comment for "Mencari g(x) jika diketahui (fog)(x) = 10x - 5 dan f(x) = 2x + 1"