Domain atau daerah asal bisa ditentukan dengan mengetahui bentuk dari persamaan yang diberikan. Syaratnya bisa dicek dibawah..
Dan untuk persamaan kita kali ini adalah berbentuk pecahan..
Soal :
1. Tentukanlah domain dari persamaan berikut,
Perhatikan soal diatas, bentuknya pecahan..
Ada salah satu syarat pecahan yang tidak boleh dilupakan, yaitu bagian penyebut (bagian bawahnya) tidak boleh sama dengan nol.
Jadi penyebutnya ≠ 0
Penyebut soal diatas adalah "x + 2"
Kita bisa kerjakan :
x + 2 ≠ 0
x ≠ -2
Jadi, agar persamaan diatas memiliki nilai, maka x tidak boleh sama dengan -2.
Ketika penyebut pecahan bernilai 0, maka hasilnya adalah tidak terdefinisi (∞).
Terus domainnya berapa?
Ini mudah, sekarang kita bisa menentukan domainnya karena nilai "x" sudah diketahui tidak boleh sama dengan -2.
HP = {x| x ≠ -2, x E real}
Cara bacanya bisa seperti ini :
" Nilai domainnya adalah x tidak boleh sama dengan -2, dan x adalah anggota (E) bilangan real"
Jadi selain -2, nilai "x" apapun boleh digunakan..
Soal :
2. Tentukanlah domain dari persamaan berikut,
Syaratnya masih sama dengan soal pertama, jadi penyebutnya ≠ 0
Langsung dikerjakan :
2x - 6 ≠ 0
2x ≠ 6
Jadi, agar persamaan diatas memiliki nilai, maka x tidak boleh sama dengan 3.
Ketika "x" diganti dengan 3, hasilnya tidak terdefinisi atau eror.
Jadi domain persamaan diatas adalah :
= {x|x ≠ 3, x E real}
Selain 3, nilai x apapun bisa digunakan untuk persamaan diatas. Itulah domain yang dimaksud dari soal ini..
Dan untuk persamaan kita kali ini adalah berbentuk pecahan..
Soal :
1. Tentukanlah domain dari persamaan berikut,
Perhatikan soal diatas, bentuknya pecahan..
Ada salah satu syarat pecahan yang tidak boleh dilupakan, yaitu bagian penyebut (bagian bawahnya) tidak boleh sama dengan nol.
Jadi penyebutnya ≠ 0
Penyebut soal diatas adalah "x + 2"
Kita bisa kerjakan :
x + 2 ≠ 0
x ≠ -2
Jadi, agar persamaan diatas memiliki nilai, maka x tidak boleh sama dengan -2.
Ketika penyebut pecahan bernilai 0, maka hasilnya adalah tidak terdefinisi (∞).
Terus domainnya berapa?
Ini mudah, sekarang kita bisa menentukan domainnya karena nilai "x" sudah diketahui tidak boleh sama dengan -2.
HP = {x| x ≠ -2, x E real}
Cara bacanya bisa seperti ini :
" Nilai domainnya adalah x tidak boleh sama dengan -2, dan x adalah anggota (E) bilangan real"
Jadi selain -2, nilai "x" apapun boleh digunakan..
Soal :
2. Tentukanlah domain dari persamaan berikut,
Syaratnya masih sama dengan soal pertama, jadi penyebutnya ≠ 0
Langsung dikerjakan :
2x - 6 ≠ 0
- pindahkan -6 ke ruas kanan menjadi +6
2x ≠ 6
- untuk mendapatkan x, bagi 6 dengan 2
x ≠ 6 : 2
x ≠ 3
Jadi, agar persamaan diatas memiliki nilai, maka x tidak boleh sama dengan 3.
Ketika "x" diganti dengan 3, hasilnya tidak terdefinisi atau eror.
Jadi domain persamaan diatas adalah :
= {x|x ≠ 3, x E real}
Selain 3, nilai x apapun bisa digunakan untuk persamaan diatas. Itulah domain yang dimaksud dari soal ini..
Baca juga :



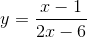

Post a Comment for "Mencari Domain (Daerah Asal) Dari 1/(x+2)"