Sebelumnya kita sudah membahas soal tentang vektor yang tegak lurus. Untuk artikelnya bisa dibaca di link ini ya : Vektor A (2, 3, 4) Tegak Lurus Vektor B (1, p, 1). Berapakah Nilai p?
Dan sekarang kita akan membahas dua vektor yang saling sejajar. Rumusnya tentu saja berbeda dengan yang tegak lurus.
Kita bahas lebih detail lagi.
Penerapan konsep
Misalkan ada dua vektor yang sejajar, katakanlah vektor A dan vektor B. Maka kedua vektor itu harus memenuhi hubungan berikut :
A.p = B
- A = vektor A
- B = vektor B
- p = faktor pengali
Untuk nilai p ini bisa positif atau negatif.
Kemudian :
- Misalkan vektor A = (a₁, a₂, a₃) dan vektor B = (b₁, b₂, b₃)
Maka, semua bagian pada vektor A dikali dengan p.
Terakhir, kita mendapatkan hubungan seperti ini :
Nah...
Hubungan inilah yang akan membantu kita dalam menyelesaikan soal vektor yang sejajar.
Contoh soal
Setelah jelas dengan konsepnya, sekarang giliran kita untuk mencoba contoh soal agar semakin paham dengan materi vektor sejajar.
Soal :
1. Diketahui vektor A = (x-1)i + yj - 2xk sejajar dengan Vektor B = 4i + 6j - 12k.
Hitunglah vektor A!
1. Diketahui vektor A = (x-1)i + yj - 2xk sejajar dengan Vektor B = 4i + 6j - 12k.
Hitunglah vektor A!
Mari kita tuntaskan!!
Ikuti konsep yang sudah dijabarkan di atas.
Ingat!!
p adalah angka pengali yang belum diketahui nilainya. Jadi biarkan saja dulu.
Dalam perhitungan, huruf penanda vektor seperti i, j dan k tidak perlu dipakai. Agar lebih mempermudah.
Ok...
Akhirnya kita mendapatkan tiga buah persamaan.
- (x-1)p = 4 ....(1)
- yp = 6 ....(2)
- -2xp = -12 ...(3)
Selanjutnya, untuk soal seperti ini, kita harus menentukan langkah yang tepat. Yaitu menggunakan persamaan (1) dan (3) dulu.
Mengapa?
Karena kedua persamaan tersebut mengandung x, sedangkan persamaan (2) tidak ada variabel x.
Itulah alasannya.
Terus kedua persamaan itu diapakan?
Kita bandingkan.
(x-1)p = 4
-2xp = -12
Keduanya dibandingkan, bentuknya seperti ini.
Langkahnya :
- p bisa dicoret
- tanda minus bisa di coret karena penyebut ruas kanan dan kiri masing-masing ada minus.
- Kalikan silang (x-1) dengan 12 dan 4 dengan 2x. Ini untuk menghilangkan bentuk pecahan
- Bukan kurung (x-1) dengan mengalikan 12.
Sehingga kita mendapatkan nilai dari x = 3.
Masukkan nilai x ini ke vektor A, sehingga menjadi :
A = (x-1)i + yj - 2xk
- x = 3
A = (3-1)i + yj - 2.3k
A = 2i + yj - 6k
Mencari nilai y
Di atas, nilai y belum ditemukan.
Kita akan gunakan bantuan dari persamaan (1) atau (3).
Bebas pilih salah satu.
Kita gunakan yang (1).
(x-1)p = 4
- x = 3
(3-1)p = 4
2p = 4
p = 2.
Kita memang harus mencari nilai p lebih dulu sebelum bisa menemukan nilai y.
Untuk mendapatkan nilai y, gunakan persamaan (2).
yp = 6
- p = 2
2y = 6
y = 3.
Menuliskan vektor A
Yap...
Akhirnya semua sudah diperoleh dan sekarang kita bisa menuliskan vektor A.
A = 2i + yj - 6k
- y = 3
A = 2i + 3j - 6k
Nah...
Itulah vektor A.
Baca juga ya :



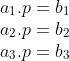



Post a Comment for "Vektor A = (x-1)i + yj - 2xk sejajar dengan Vektor B= 4i + 6j - 12k. Hitunglah vektor a!"