Untuk soal ini, kita lakukan pengubahan bentuk soalnya sedikit, sehingga bisa di-integral-kan dan akhirnya menemukan hasilnya.
Contoh soal
Soalnya bisa dilihat di bawah ini!!
Baik...
Mari kita jawab soalnya...
Soalnya diubah dulu, masing-masing suku pada pembilang dibagi oleh x².
Mengubahnya seperti ini membuat pengerjaan soal lebih mudah.

Terus, bagi semuanya dengan x² yaitu dengan menyederhanakan variabel x.
Untuk 2/x² dibiarkan seperti itu karena di bagian pembilang tidak ada variabel x.
Selanjutnya, bawa x² yang menjadi pembagi 2 ke pembilang, sehingga pangkatnya menjadi bentuk negatif.
Tujuan pengubahan ini agar proses integral semakin dimudahkan.
Ingat lagi rumus pengintegralan ya!!
Sebenarnya, sampai disini jawabannya sudah jelas.
Tapi jika dipilihan jawaban tidak ada, perlu dilakukan pengubahan lanjutan.
Setiap suku disamakan penyebutnya, dengan membuatnya memiliki penyebut x.
Nah...
Seperti itulah jawabannya.
Semoga membantu ya!!
Baca juga ya :



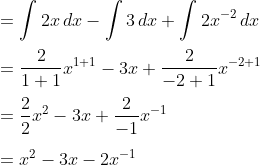


This comment has been removed by a blog administrator.
ReplyDelete