Home / Limit

Menghitung limit x→0 (2x)/(2sinx+sin2x)

Post a Comment

Ketika berhubungan dengan limit trigonometri yang mendekati nol, maka ada aturan atau sifat yang sangat membantu.


Dengan menggunakan sifat tersebut, kita bisa mencari jawaban yang diinginkan dengan tepat. Sifatnya seperti apa?

Konsep

Nah...
Inilah sifat yang membantu kita menyelesaikan soal seperti ini.




Pahami ya sifatnya.
Karena pada soal hanya ada bentuk sin, jadi hanya sifat sin yang diberikan di sini.

Contoh soal

Sekarang kita coba soalnya.


Soal :

1. Hitunglah nilai dari : 


Ada dua cara untuk menyelesaikan soal ini.


Cara pertama

Tulis lagi soalnya.



  • Setiap suku dibagi dengan x
  • Untuk apa? 
    Untuk membuat bentuk sin x menjadi bentuk yang mirip dengan sifat yang sudah dijelaskan di atas.



Ingat lagi ya!




Kemudian :



Nah...
Hasilnya adalah ½.


Cara kedua

Di sini kita mengubah bentuk sin2x.


  • sin 2x = 2.sin x.cos x
    Ini adalah sifat trigonometri yang lain.
    Hafalkan ya



  • Sekarang faktorkan penyebutnya
  • (2sin x) bisa dikeluarkan, sehingga bentuknya seperti di atas.


  • Kita ubah lagi bentuknya menjadi dua pecahan berbeda.


  • Ingat lagi sifat trigonometri di atas, x/sin x menjadi 1 ketika limitnya mendekati nol
  • cos 0 = 1
Dan hasilnya diperoleh ½, sama dengan cara pertama.
Semoga membantu ya...


Baca juga ya :
Location:

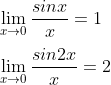
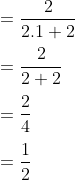
Post a Comment for "Menghitung limit x→0 (2x)/(2sinx+sin2x)"