Letak suatu titik terhadap lingkaran, bisa ditentukan dengan sangat mudah. Yaitu memasukkan titik tersebut ke dalam persamaan lingkarannya.
Syarat yang harus dipenuhi
Letak suatu titik pada lingkaran akan mengikuti syarat-syarat berikut. Misalkan rumus sebuah lingkaran adalah :
x² + y² = a
Syarat yang harus dipenuhi adalah :
- Jika x² + y² < a, maka titik itu berada di dalam lingkaran
- Jika x² + y² = a, maka titik itu tepat berada pada lingkaran (tepat berada pada garis lingkarannya)
- Jika x² + y² > a, maka titik itu berada di luar lingkaran
Sudah mengerti dengan syaratnya?
Jika masih bingung, langsung saja lihat contoh soal di bawah ini untuk membuat anda lebih mengerti lagi.
Soal
Yuk lihat soalnya!
Soal :
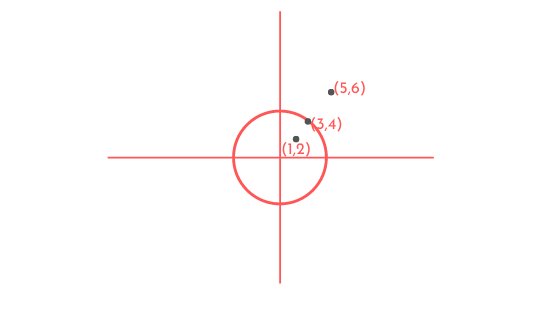
1. Sebuah lingkaran dengan persamaan x² + y² = 25, tentukanlah posisi titik (1,2), (3,4) dan (5,6) terhadap lingkarannya!
1. Sebuah lingkaran dengan persamaan x² + y² = 25, tentukanlah posisi titik (1,2), (3,4) dan (5,6) terhadap lingkarannya!
Dengan menggunakan syarat yang sudah diberikan di atas, kita bisa langsung mengeksekusi soalnya. Mari lanjutkan!!
Titik (1,2)
Cek titiknya satu per satu dan kita mulai dari yang pertama, titik (1,2).
Titiknya (1,2), berarti :
- x = 1
- y = 2
Ganti x dan y pada persamaan lingkaran dengan nilai di atas.
x² + y² = 25
- x = 1
- y = 2
1² + 2² ... 25
- Gunakan titik-titik dulu karena kita belum tahu hasilnya yang di ruas kiri.
1 + 4 ... 25
5 ... 25
Hasil yang di ruas kiri 5 sedangkan yang di ruas kanan 25.
Sehingga yang di ruas kiri kurang dari yang kanan.
Jadi...
5 < 25.
Karena kita mendapatkan tanda kurang, maka titik (1,2) berada di dalam lingkaran.
Titik (3,4)
(3,4) berarti :
- x = 3
- y = 4
Masukkan nilai x dan y ke dalam persamaan lingkaran
x² + y² = 25
- x = 3
- y = 4
3² + 4² ... 25
- Masih menggunakan titik-titik karena kita belum tahu hasil di ruas kiri
9 + 16 ... 25
25 ... 25
Yap...
Hasil di ruas kiri dan kanan sama.
Sehingga :
25 = 25.
Dan kita peroleh bahwa titik (3,4) berada pada lingkaran.
Titik (5,6)
(5,6) :
- x = 5
- y = 6
Masukkan ke dalam rumus persamaan lingkaran
x² + y² = 25
5² + 6² ... 25
25 + 36 ... 25
61 ... 25
Hasil di ruas kiri lebih besar dari ruas kanan.
Sehingga :
61 > 25
Karena ruas kiri lebih besar dari ruas kanan, maka titik (5,6) berada di luar lingkaran.
Bagaimana, mudah bukan??
Untuk gambar posisi masing-masing titik, bisa dilihat di atas.
Seperti itulah letaknya.
Baca juga ya :

Post a Comment for "Cara menentukan apakah suatu titik berada ditengah, pada dan luar lingkaran"