Ok..
Ini adalah salah satu soal bertipe ujian masuk perguruan tinggi negeri. Bagi yang masih bingung, mari ikuti langkah pengerjaannya.
Bedah soal
Terlihat soalnya sangat singkat ya dan sangat sedikit informasi yang bisa diulik. Tapi tenang, dengan melihat kembali konsep fungsi, kita bisa mendapatkan informasi penting yang membantu menemukan jawaban.
Fungsi di atas adalah fungsi kuadrat.
Mengapa?
Karena pangkat variabel x paling tinggi adalah 2.
Karena pangkat variabel x paling tinggi adalah 2.
Nanti grafiknya berbentuk parabola.
Menyinggung sumbu x
Inilah kunci penting soal ini, yaitu menyinggung sumbu x.
Apasih artinya??
Menyinggung sumbu x, berarti fungsi ini hanya memiliki satu penyelesaian saja. Alias nilai x-nya hanya ada satu.
Beda jika fungsinya memotong sumbu x, akan memiliki dua penyelesaian.
Info penting lainnya adalah, nilai x tempat persinggungan di sumbu x ini akan menjadi sumbu simetri fungsi.
Ya, sumbu simetrinya.
Dari kalimat "menyinggung sumbu x", kita bisa mendapatkan dua informasi sekaligus.
- Titik puncak grafik adalah (⅔,0).
Karena pas di sumbu x, maka nilai y pastilah nol - Sumbu simetrinya adalah ⅔
Mengapa grafiknya terbuka ke atas?
Kesimpulan ini bisa diteliti dari persamaan yang diketahui.
F(x) = a²x²-12x+c²
Untuk menentukan grafik terbuka ke atas atau ke bawah, kita bisa melihat koefisien dari x². Lebih mudahnya angka di depan x².
Yaitu a².
Berapapun nilai a, hasilnya pasti positif, karena dipangkat dua.
Dari aturannya :
- Jika koefisien x² positif, grafik terbuka ke atas
- Jika koefisien x² negatif, gratif terbuka ke bawah
Sehingga, grafik fungsi soalnya akan terbuka ke atas.
Jelas ya??
Soal
Setelah membaca penjelasan di atas, kita bisa mengerjakan soalnya dan mendapatkan jawaban yang diminta.
Soal :
1. Diketahui fungsi f(x) = (x) = a²x²-12x+c² menyinggung sumbu x di titik ⅔. Hitunglah nilai dari a²-c²!
1. Diketahui fungsi f(x) = (x) = a²x²-12x+c² menyinggung sumbu x di titik ⅔. Hitunglah nilai dari a²-c²!
Sumbu simetri grafik = ⅔
Pergerakan dimulai dari data ini.
Gunakan rumus sumbu simetri.
x = -b/2a
Dari persamaan fungsi di atas, kita bisa mendapatkan nilai dari masing-masing koefisien.
- a = a² (angka di depan x²)
- b = -12 ( angka di depan x)
- c = c² (angka yang tidak mengandung variabel)
Nilai x = ⅔, karena x sebagai sumbu simetri.
- Kalikan silang untuk menghilangkan bentuk pecahan.
- Kalikan 2 dengan 2a²
- Kalikan 12 dengan 3
2×2a² = 12×3
4a² = 36
- Untuk mendapatkan a², bagi 36 dengan 4
a² = 36÷4
a² = 9
Biarkan saja dalam bentuk a², tidak perlu diakarkan.
Mencari c²
Nilai a² sudah diketahui dan kita masukkan nilai ini ke dalam persamaan fungsi awal.
f(x) = a²x²-12x+c²
- ganti a² dengan 9
f(x) = 9x²-12x+c²
Puncak grafik (⅔,0)Inilah yang digunakan untuk mencari c²
Data ini sangat membantu kita dalam menemukan c². Ganti x dengan ⅔ dan ganti f(x) dengan 0.
0 = 9(⅔)² - 12(⅔) + c²
0 = 9(⁴∕₉) - 8 + c²
0 = 4 - 8 + c²
0 = -4 + c²
- Pindahkan -4 ke ruas kiri menjadi +4
4 = c²
Nilai a² dan c² sudah ditemukan dan sekarang kita bisa menghitung hasilnya.
Mencari a²-c²
= a² - c²
- a² = 9
- c² = 4
= 9 - 4
= 5
Nah...
Itulah jawabannya.
Baca juga ya :


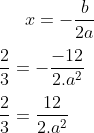
Post a Comment for "Fungsi f(x) = a²x²-12x+c² menyinggung sumbu x di titik ⅔. Hitung nilai a²-c²!"