Home / Fungsi

Jika mx + ny = 1, maka hitunglah nilai maksimum dari xy!

Post a Comment

Nah...
Ini adalah salah satu soal yang muncul dalam seleksi penerimaan mahasiswa baru. Kesan pertamanya bagaimana?

Bingung?


Ok...
Tenang dulu ya!!
Kita akan bahas soalnya.

Soal

Soalnya seperti ini.

Soal :

1. Diketahui sebuah persamaan mx + ny = 1. Hitunglah nilai maksimum dari "xy"!


Ada dua cara yang bisa ditempuh.


Cara pertama

Diketahui persamaan :
  • mx + ny = 1

Kita diminta untuk mendapatkan nilai maksimum dari xy.
Sudah tahu arti dari xy?
  • xy adalah hasil perkalian dari nilai x dan y.

Itulah yang akan dicari.


Mengubah persamaan dalam bentuk y

Kita ubah dulu persamaannya ke dalam bentuk y.




Menggunakan nilai maksimum dari xy

Sekarang kita masukkan ke dalam nilai yang diminta, yaitu xy.




Misalkan xy dengan f(a)

Buat xy ke dalam fungsi f(a) untuk memudahkan menurunkan. 
Ya...
Kita akan menurunkan fungsinya untuk mendapatkan nilai maksimum dari x.

Pertama, perhatikan dulu rumus penurunan berikut.



Dalam rumus di atas :
  • u = x-mx²
  • v =n

Turunkan masing-masing terhadap x.

u = x-mx²
u' = 1 - 2mx

v = n
v' = 0

Turunan v menjadi 0 karena pada v tidak ada x. Sehingga ketika diturunkan ke x, hasilnya adalah nol.

Nah...
Kita sudah mendapatkan turunan dari masing-masing u dan v.
  • u'= 1-2mx
  • v' = 0


Menurunkan f(a)

Sekarang kita turunkan f(a) terhadap x.



  • (x-mx²)0
    (x-mx²)×0 = 0
  • n dan n² sama-sama bisa dibagi n
    Sehingga n di bagian atas (pembilang) hilang sedangkan n² menjadi n


Mencari x dengan membuat f '(a) = 0

Untuk mendapatkan nilai x, kita buat f '(a) = 0



  • 0 dikalikan silang dengan n, hasilnya 0
  • Dan kita tidak memiliki bentuk pecahan lagi

Nah...
Nilai x sudah diperoleh.



Mencari nilai y

Masih ingat dengan rumus y dari hasil pengubahan mx+ny =1?
Masukkan nilai x ke sana.



Nah...
Masukkan nilai x ke dalam persamaan di atas.

  • x = 1/2m



  • m di atas dan di bawah bisa sama-sama dicoret dan hilang

Ok...
Nilai y juga sudah diperoleh.


Mencari nilai xy

Kita sudah mendapatkan masing-masing nilai x dan y.




Selanjutnya kita cari nilai xy.




Nah...
Itulah nilai maksimum dari xy.



Cara kedua

Untuk cara yang kedua ini, bisa dibilang lebih cepat dan pastinya lebih mudah. Kok begitu? 
Mari kita kupas.

Lihat lagi persamaan yang diberikan pada soal.

mx + ny = 1

Bisa diartikan sebagai berikut :
  • mx jika ditambahkan dengan ny akan menghasilkan 1

Nah...
Untuk mendapatkan nilai maksimum, maka 1 harus dibagi dengan 2.
Hasilnya ½
Dibagi 2 karena hanya ada mx dan ny.

mx + ny = 1
½   + ½  = 1

Dari bentuk di atas bisa disimpulkan sebagai berikut :
  • mx haruslah ½
  • ny haruslah ½

Bagaimana, sudah jelas sampai di sana?


Mencari nilai x

Kita sudah mendapatkan persamaan mx = ½




Mencari nilai y

ny = ½




Mencari nilai xy

Nah...
Nilai x dan y sama bukan dengan cara pertama?




Dan nilai xy bisa dihitung.




Nah...
Seperti itulah langkah penyelesaiannya.
Semoga membantu ya!!


Baca juga ya :
Location:

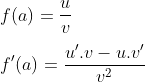
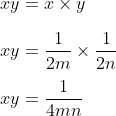
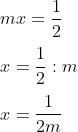
Post a Comment for "Jika mx + ny = 1, maka hitunglah nilai maksimum dari xy!"