Masih dengan soal trigonometri dan kali ini kita mengerjakan variasi soal-soalnya. Dengan memahami sifat-sifatnya, kita bisa dengan mudah mengerjakan soal.
Konsep soal
Sebelum masuk ke soalnya, kita lihat dulu konsep yang digunakan. Memahami konsepnya sangat penting, agar tidak salah dalam menentukan jawaban.
Kunci soal :Sudut A adalah sudut tumpul
Sudut tumpul menjadi clue penting, jika tidak hati-hati, pasti mendapatkan jawaban yang salah.
Ada apa dengan sudut tumpul?
Sudut tumpul adalah sudut yang terletak di kuadran kedua, yaitu antara 90⁰ sampai 180⁰.
Nilai-nilai dari sin, cos dan tan di kuadran ini adalah :
- sin bernilai positif (+)
- cos bernilai negatif (-)
- tan bernilai negatif (-).
Nah...
Sudah jelas sampai di sana?
Jangan lupa dengan tanda soalnya ya!!
Rumus yang digunakan
Kita akan menggunakan hubungan rumus antara sin dan cos dulu. Karena kita harus mencari sin agar bisa mendapatkan tan sudut yang dimaksud.
sin²A + cos²A = 1
Ini adalah sifat trigonometri umum yang wajib diketahui. Hafalkan rumus ini ya, karena sering dipakai dalam banyak perhitungan.
Contoh soal
Ok...
Kita coba contoh soalnya.
Soal :
1. Diketahui cos²A = ⁴∕₅ dan A adalah sudut tumpul, hitunglah tan A!
1. Diketahui cos²A = ⁴∕₅ dan A adalah sudut tumpul, hitunglah tan A!
Kita cari dulu sin A.
Mencari sin A
Gunakan sifat trigonometri di atas untuk mendapatkan sin A.
Diketahui pada soal :
- cos²A = ⁴∕₅
- Pindahkan ⁴∕₅ ke ruas kanan menjadi -⁴∕₅
- Ubah 1 menjadi ⁵∕₅ agar penyebutnya sama dengan ⁴∕₅
- Kemudian kita mendapatkan sin²A = ¹∕₅
- Untuk mendapatkan sin A, maka ¹∕₅ harus diakarkan.
Ok...
Kita sudah mendapatkan sin A.
Ingat!Sin pada sudut tumpul bernilai positif (dikuadran II)
Mencari cos A
Setelah sin A diperoleh, sekarang giliran dari cos A.
Dari soal diketahui jika :
- cos²A = ⁴∕₅
Kita bisa mencari cos A.
Nah ingat lagi...A adalah sudut tumpul, sehingga cos-nya harus bernilai negatif.Sehingga cos A yang benar adalah -√⁴∕₅
Mencari tan A
Sin A dan cos A sudah diketahui.
Sekarang kita bisa menghitung tan A.
Ingat rumus tan ya!!tan = sin/cos.
Tan adalah hasil pembagian dari sin dan cos.
- sin A = √¹∕₅
- cos A = -√⁴∕₅
- Masukkan sin A dan cos A.
- Ingat bahwa cos A bernilai negatif karena A sudut tumpul dan ada di kuadran II.
- Tanda bagi bisa diubah menjadi perkalian dan pecahan di belakang tanda bagi ditukar posisinya.
- Pecahan dibelakang tanda bagi, yaitu ⁴∕₅ berubah menjadi ⁵∕₄
Dan kitapun mendapatkan nilai dari tan A, yaitu -½.
Bagaimana, sudah dimengerti ya??
Semoga membantu...
Alternatif lain
Di atas kita sudah mendapatkan nilai dari :
- sin²A = ¹∕₅
- cos²A = ⁴∕₅
Dengan menggunakan ini, kita bisa mencari tan-nya juga, tanpa perlu mencari sin A yang hasilnya dalam bentuk akar.
Langkahnya seperti ini.
- Tanda bagi diubah menjadi perkalian dan pecahan di belakang tanda bagi ditukar posisinya
- Untuk mendapatkan tan A, akarkan ¼
- Hasil pengakaran adalah plus dan minus.
Nah ingat lagi!!
Tan di kuadran II adalah negatif, jadi pilihlah yang hasilnya negatif.
Sehingga tan A = -½
Baca juga ya :





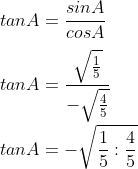
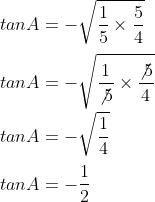


Post a Comment for "Jika cos²A = 4/5 dan A adalah sudut tumpul, hitunglah tan A!"