Untuk menjawab soal ini, kita harus mengerti dengan konsep dua garis lurus yang saling tegak lurus. Apa yang menjadi hubungan keduanya.
Konsep garis saling tegak lurus
Jika ada dua garis lurus yang saling tegak lurus, maka konsep ini berlaku.
Hasil kali gradien keduanya adalah -1.
m₁ × m₂ = -1
Keterangan :
- m₁ = gradien garis pertama
- m₂ = gradien garis kedua
Soal
Ok...
Sekarang kita masuk ke soalnya.
Soal :
1. Nilai k yang membuat garis : kx - 3y = 10 tegak lurus dengan y = 3x - 3 adalah...
1. Nilai k yang membuat garis : kx - 3y = 10 tegak lurus dengan y = 3x - 3 adalah...
Mencari gradien garis pertama
Garis pertama kita ambil : kx - 3y = 10
Untuk mendapatkan gradien, kita harus membuat persamaan dalam bentuk y.
Seperti ini :
kx - 3y = 10
- pindahkan kx ke ruas kanan menjadi -kx
-3y = -kx + 10
- 10 tidak dipindah, karena kita ingin membuat persamaan dalam bentuk y.
- Sehingga hanya yang mengandung y ada di ruas kiri
- Semua suku dibagi dengan -3
- Mengapa -3?
Untuk membuat y sendiri dan tidak ada angka lagi di depannya. Atau lebih tepatnya, y memiliki angka 1 sebagai koefisien
Gradien garis pertama (m₁) adalah koefisien x, atau bilangan di depan x.
Sehingga m₁ = k/3
Nah, seperti itulah cara mencari gradien dari sebuah persamaan garis yang diketahui.
Mencari gradien garis kedua
Sekarang garis kedua adalah y = 3x - 3
Perhatikan persamaan garisnya :
y = 3x - 3
- Koefisien dari y sudah 1 (tidak terlihat ada angka di depan y)
- Dan y sudah sendiri di ruas kiri
- Jadi persamaannya sudah benar dan sekarang kita bisa mendapatkan gradien garis kedua
y = 3x - 3
Gradien garis kedua adalah angka di depan x, yaitu 3 (yang di warna merah).
m₂ = 3
Mencari nilai k
Kita sudah mendapatkan gradien masing-masing garis.
Sekarang bisa mendapatkan nilai k dengan menggunakan konsep garis lurus.
m₁ × m₂ = -1
Diketahui :
- m₁ = k/3
- m₂ = 3
Ingat!!
Hasil kali kedua gradien adalah -1 jika saling tegak lurus.
m₁ × m₂ = -1
Diperoleh nilai k = -1.
Inilah jawaban yang diminta pada soal.
Trik mencari gradien diketahui persamaan garis
Bagi yang masih bingung cara mencari gradien dari suatu persamaan garis, saya berikan contohnya lagi ya.
Untuk mendapatkan gradien, maka persamaannya harus berbentuk seperti ini :
y = mx + c
Maksudnya :
- y harus sendiri di ruas kiri dan tidak boleh ada suku yang menemani
- Angka di depan y harus satu.
Itulah langkah-langkahnya.
Kita ubah 3x - 2y + 8 = 0
Pindahkan selain y ke ruas kanan
3x - 2y + 8 = 0
- Hanya yang ada y di sebelah kiri
- Jadi pindahkan 3x dan 8 ke ruas kanan
- 3x dipindah ke ruas kanan menjadi -3x
- +8 dipindah ke ruas kanan menjadi -8
-2y = -3x - 8
Membuat koefisien y menjadi 1
-2y = -3x - 8
Kita sudah mendapatkan bentuk di atas pada langkah pertama. Sekarang membuat koefisien y menjadi satu atau tidak terlihat angka di depan y.
Bentuk di atas, kita masih memiliki -2 sebagai bilangan di depan y.
-2 ini harus dihilangkan.
Caranya dengan membagi semua suku dengan -2 juga, bilangan yang sama di depan y.
-2y = -3x - 8
Gradien adalah bilangan di depan x.
Gradien (m) = ³∕₂.
Nah...
Semoga membantu ya...
Baca juga ya :



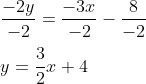
Post a Comment for "Nilai k yang membuat garis kx - 3y = 10 tegak lurus dengan y = 3x - 3 adalah..."